Elliptic Curves (Part I)

Elliptic curves are an essential part in modern day cryptography. But what are they? And how do they work? Although the theory behind Elliptic Curves is very complex, I try to delve into this subject here. I’m not a mathematician, so I do not know all the ins and out, nor do I know all the details. However, I try to write down the things I know about this matter hoping this is useful to you.

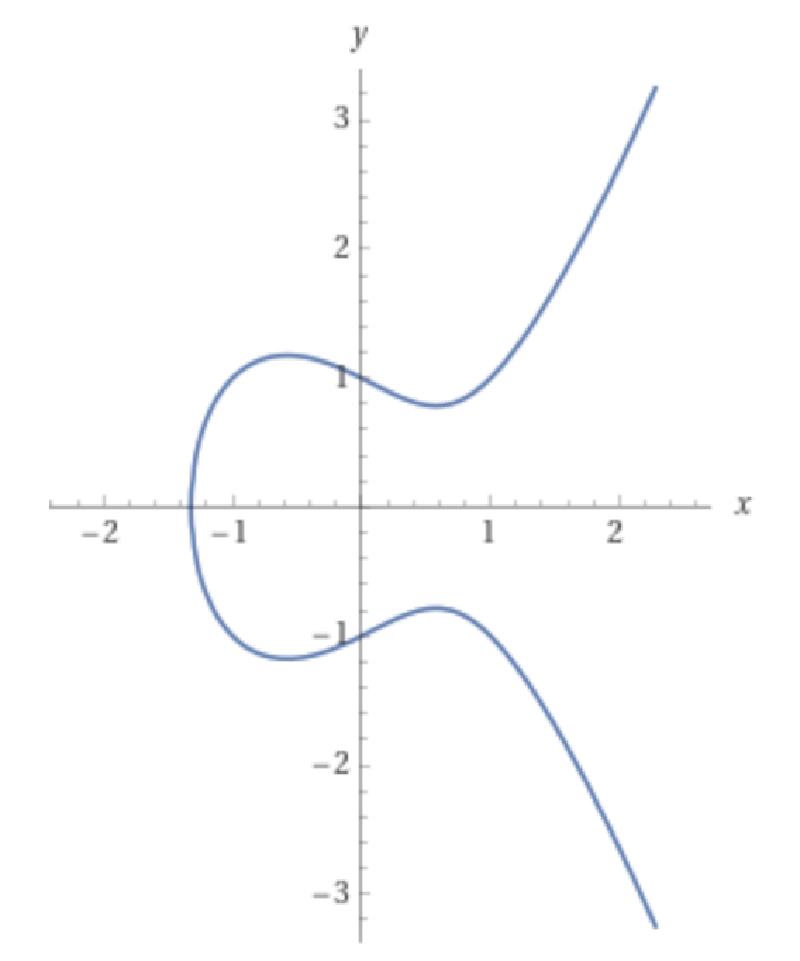
What are Elliptic Curves actually? An elliptic curve is defined by an equation of the form: $$ y^2 = x^3 + Ax + B $$

and is defined in the $\R^2$ space (the x-y plane). They look as follows (A = -1, B = 1):

elliptic curve for a= -1, b = 1

Note that not all A’s and B’s can be used to produce a valid Elliptic Curve. Only A’s and B’s that fulfil the following criteria are valid:

$$-16 (4A^3 + 27 B^2) \ne 0$$

Abelian Groups

Abe…? What? To be able to understand Elliptic Curves, we have to define and understand some complex mathematics. We begin our journey with Abelian Groups. But, I warn you, it gets more complex than this… However, hopefully it all makes sense in the end.

Abelian Groups $(\Alpha, \circ)$ is a set of elements $\Alpha$ (numbers, points, etc.), together with an operation ($\circ$) that combines two elements of this set to form a new element of that set. Huh? Actually, it’s quite easy. Let’s say $a$ and $b$ are elements of the set, and $+$ is the operation. Then we form a new element $c$ which is $c=a + b$. What are you kidding me? Is this all the fuss about Abelian Groups? Come on man! Well… there are five rules that the Abelian Group should fulfil, in order to be an actual Abelian Group:

Closure. If $a$ and $b$ are members of $\Alpha$, then $a \circ b$ is also a member of $\Alpha$
Associativity. For all $a$, $b$ and $c$ of set $\Alpha$, the following holds: $$ (a \circ b) \circ c = a \circ (b \circ c)$$
Commutativity. For all $a$ and $b$ in $\Alpha$ the following holds: $$ a \circ b = b \circ a $$
Identity Element. There exists an element $\epsilon$ in $\Alpha$ such that for all elements $a$ in $\Alpha$ the following equation holds: $$\epsilon \circ a = a \circ \epsilon = a$$
Inverse element. For each $a$ in $\Alpha$ there exists an element $b$ in $\Alpha$ such that the following equation holds ($\epsilon$ is the identity element): $$ a \circ b = b \circ a = \epsilon $$

Lets give an example: is $(\R, +)$ an Abelian group (the set of integer numbers $\R$, with the operator $+$)?

Closure: take two elements, lets say -7 and 11, is the result ($-7 + 11 = 4$) also part of $\R$? Yes!
(I just took two random values here, but you can verify that this is true for all elements of $\R$)
Associativity: Suppose we have 3 numbers: 6, 3 and -8. Is $(6 + 3) + -8$ the same as
$6 + (3 + -8)$? Yes!
Commutativity: Is -3 + 5 the same as 5 + -3? Yes!
Identity Element: Is there an element $\epsilon$ for which all elements $a$ the following is true
$\epsilon + a = a + \epsilon = a$? Yes, this is true when $\epsilon = 0$
Inverse element: For a given number, for example 2, is there an element $b$ part of $\Alpha$
for which $ 2 + b = b + 2 = 0 $? Yes, this is true when $b=-2$

So, yes, $(\R, +)$ is an Abelian Group.

Is $(\R, -)$ an Abelian Group? No, it does not fulfil the commutativity rule: $ 4 - 7 \ne 7 - 4$

Are the natural numbers $(\N, \circ)$ an Abelian Group? No, it does not fulfil the inverse element rule: Suppose $a = 8$, there exist no element in $\N$ for which $ 8 - b = b - 8 = 0 $ (Yes, for $b=-8$ this equation holds. But, -8 is not part of $\N$).

Note that the identity element $\epsilon$ for the operator $*$ is 1
($1 * a = a * 1 = a$).

Note that the elements in the set do not have to be numbers, it can also be points, vectors, etc.

Why are Abelian Groups important for Elliptic Curves? We are going to find out whether the points of an Elliptic Curve form together an Abelian Group. If so, we can do some math on those points. Whether the points of an Elliptic Curve form an Abelian Group depends on whether the 5 rules above hold, yes or no (spoiler alert: yes, they do). So for example we have to find an operator and an identity element.

But before we go further with Elliptic Curves, we have to introduce projective space first.

Projective Space

Elliptic Curves are defined in $\R^2$, but projective space relies on one extra coordinate with some additional assumptions. Se we have the following coordinate in $\R^3$ space: $$(x, y, z)$$. With two additional assumptions:

$(0, 0, 0)$ is not allowed
$(x, y, z)$ is the same as $(\lambda x, \lambda y, \lambda z)$, where $\lambda$ can be any number except 0.

If we fill in any value for $\lambda$ we see that we get a line running through the origin.

Since $(\lambda x, \lambda y, \lambda z)$ is the same for any value of $\lambda$ (except zero) we can rewrite this to $[x:y:z]$ for convenience.

So, if we have for example $[1:2:3]$ this represents a line running through the origin. Also, $[5:-9:2]$ represents a line running through the origin, and $[7: -3: 14]$, etc.

We now can try to define the entire 3d space. However, there are some tricky issues to consider.

If we have $[x:y:z]$ and $z \ne 0$, we can divide every coordinate by $z$, so we get $[x/z:y/z:1]$. Since $\lambda$ can be any number, it can also be $\lambda = 1 / z$, then we get $[x: y: 1]$. This is the projection plane where z = 1. All lines running through the origin, also run through the plane defined at $z = 1$. So, every line has a projection point on $z = 1$, namely $(x,y)$.

Cool, but what happens when $z = 0$? Obviously, we cannot divide by z. What can we do? In this case, we can do the same trick, but now for y. So if we have $[x:y:0]$ and divide by y, ($y \ne 0)$ we get: $[x: 1: 0]$. Remember that $\lambda$ can be anything, so $x/y$ is the same as $x$ ($\lambda$ is $1/y$).
This represents a line at y = 1, and z = 0. How cool is that? Can you guess the last problem? What if y = 0?

If y is zero, we have $[x: 0: 0]$. And since x can be divided by x ($x \ne 0$) we get $[1: 0: 0]$

And… what if x = 0? Aha! No, that is not possible, because we assumed $(0, 0, 0)$ is not allowed by definition.

Now we have the entire 3d projection space defined. Let’s go back to the elliptic curve.

Elliptic Curve in projective space

Remember the Elliptic Curve being defined as: $ y^2 = x^3 + Ax + B $ In projective space we just add an extra coordinate, $z$.

Can we project the elliptic curve on $z=1$?
Of course, then we have: $[x/z:y/z:1]$ which results in:

$$ \begin{gather*} (y/z)^2 = (x/z)^3 + Ax/z + B \newline y^2 / z^2 = x^3 / z^3 + Ax / z + B \newline z = 1 \newline y^2 = x^3 + Ax + B \end{gather*} $$

So, when the Elliptic Curve is projected on the $z=1$ plane, we have the same Elliptic Curve! Cool!

But… what if z = 0? Then we have two cases, remember?
$[x:1:0]$ for $y \ne 0$, and
$[1:0:0]$ for $y=0$.

Let’s consider them both, but first rewrite $(y/z)^2 = (x/z)^3 + Ax/z + B$ (the Elliptic Curve in projective coordinates) a bit for convenience.
Multiply both sides with $z^3$, then we get:

$$y^2z = x^3 + Axz^2 + B z^3$$

For $[1:0:0]$ we have:

$$0 \ne 1 + 0 + 0$$

Which is not part of the curve, so we can ignore this.

For $[x:1:0]$ we have:

$$0 = x^3 + 0 + 0$$

Which is only true for $x=0$, so we get $[0:1:0]$

So, now we can completely define the Elliptic Curve in projective space:
$y^2z = x^3 + Axz^2 + B z^3$, for z = 1
$[0:1:0]$, for z = 0

But what does this actually mean?

Remember that we project the curve on $z=1$? But suppose we project the curve on $t$ instead. So, we have:
$[x/t:y/t:z/t]$

Also remember that this represents a line running through the origin. But what happens at the “end” of the line, at infinity?

For this we make $t$ bigger and bigger towards infinity. Meaning the projecting plane, parallel to the xy-plane, will move further away from the origin. When $t$ approaches infinity, $z/t$ moves towards 0. Which is our point $[0:1:0]$ in case of Elliptic Curves.

Adding points on the Elliptic Curve

We define the $+$ operator to be (later we will verify whether this holds given the five rules of the Abelian Group):

$ P + Q + R = 0 $

Where $0$ is the point at infinity: $[0:1:0]$

If we look at the graph of an Elliptic Curve, we can draw a straight line that crosses the curve at one, two or three points. We define two points, $P = (x_p,y_p)$ and $Q = (x_q,y_q)$, and try to find $R$ (if any).

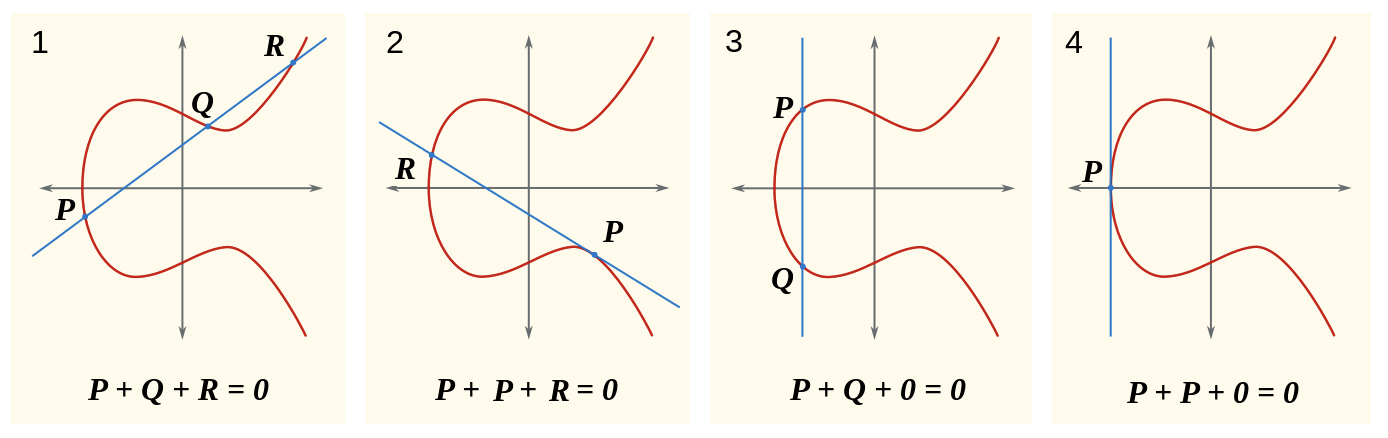
elliptic curve with an intersection line

We can distinguish 4 cases:

Case 1: $x_p \ne x_q$

$ P + Q + R = 0 $

The slope and intercept of the line is:

$\lambda = {y_q - y_p \over x_q - x_p}$
$\nu = y_p - \lambda x_p$

We can find the intersection of the curve with the line by solving:

$(\lambda x + \nu)^2 = x^3 + Ax + B$

Which is equivalent to:

$x^3 - \lambda^2 x^2 - 2 \lambda \nu x + Ax + B - \nu^2 = 0$

We already know that P, Q and R are on the curve, this equation has its roots at exactly the same x values as: $(x - x_p)(x - x_q)(x - x_r)$

Expanding this expression yields: $x^3 + (-x_p - x_q - x_r)x^2 + (x_p x_q + x_p x_r + x_q x_r)x - x_p x_q x_r $

Now, compare this to: $x^3 - \lambda^2 x^2 - 2 \lambda \nu x + Ax + B - \nu^2$

We see that $-\lambda^2$ must be equal to $(-x_p - x_q - x_r)$
(We also see that $x^3$ is correct, and we see that $A - 2 \lambda \nu = (x_p x_q + x_p x_r + x_q x_r)$,
and we see that $B - \nu^2 = - x_p x_q x_r$)

We can rewrite:
$-\lambda^2 = (-x_p - x_q - x_r)$

Into:
$x_r = \lambda^2 - x_p - x_q$

Using the line equation $y = \lambda x + \nu$ we can solve $y_r$:
$y_r = \lambda x_r + \nu$

Knowing $x_r$, this results in:

$y_r = \lambda (\lambda^2 - x_p - x_q) + \nu = \lambda^3 - \lambda (x_p + x_q) + \nu$

We can rewrite $\nu$, since $\lambda = {y_q - y_p \over x_q - x_p}$:
$\nu = y_p - ({y_q - y_p \over x_q - x_p}) x_p = {x_q y_p - x_p y_q \over x_q - x_p}$

Since $P + Q + R = 0$, we can rewrite this into $P+Q=-R$,
which results in: $P+R = (x_r, - y_r)$

Filling in $x_r$ and $y_r$:

$P+R = (\lambda^2 - x_p - x_q, -\lambda^3 + \lambda (x_p + x_q) - \nu)$

Where:
$\lambda = {y_q - y_p \over x_q - x_p}$
$\nu = {x_q y_p - x_p y_q \over x_q - x_p}$

Case 2: $x_p = x_q$ and $y_p = y_q \ne 0$

$ P + P + R = 0 $

When $x_p = x_q$ and $y_p = y_q \ne 0$, the points $P$ and $Q$ are equal (but not located on the x-axis). In this case $R = -2P$ and the slope of the line is the tangent running through $P$.

The slope and intercept of this line is:

$ \lambda = {3x_p^2 + A \over 2y_p}$
$\nu = y_p - \lambda x_p$

We can rewrite $\nu$, since $\lambda = {3x_p^2 + A \over 2y_p}$:
$\nu = y_p - ({3x_p^2 + A \over 2y_p}) x_p = {2 y_p^2 - 3 x^3 +Ax \over 2y}$
Filling in the definition of the Elliptic Curve:
$\nu = {-x_p^3 + Ax_p + 2B \over 2 y_p}$

Following the same strategy as in Case 1, we get:

$x_r = \lambda^2 - 2 x_p$
$y_r = \lambda^3 - 2 \lambda x_p + \nu$

Since $2P + R = 0$, we can rewrite this into $2P=-R$,
which results in: $2P = (x_r, - y_r)$

Filling in $x_r$ and $y_r$:

$2P = (\lambda^2 - 2x_p, -\lambda^3 + 2 \lambda x_p - \nu)$

Where:
$\lambda = {3x_p^2 + A \over 2y_p}$
$\nu = {-x_p^3 + Ax_p + 2B \over 2 y_p}$

Case 3: $x_p = x_q$ and $y_p = -y_q$

$P + Q + 0 = 0$

In this case the line through P and Q is vertical, and P and Q are mirrored along the x-axis. However, not on the x-axis.

Case 4: $x_p = x_q$ and $y_p = y_q = 0$

$P + P + 0 = 0$

In this case P = Q, and both are located on the x-axis. The line through P is the tangent and also vertical.

Final add definition

So we can conclude that:

if $P \ne Q$ and $x_p$ = $x_q$, then $P + Q = 0$
if $P = Q$ and $y_p = y_q = 0$, then $2P = 0$
if $P \ne Q$ and $x_p \ne x_q$, then
$\lambda = {y_q - y_p \over x_q - x_p}$
$\nu = {x_q y_p - x_p y_q \over x_q - x_p}$
if $P = Q$ and $y_p = y_q \ne 0$, then
$\lambda = {3x_p^2 + A \over 2y_p}$
$\nu = {-x_p^3 + Ax_p + 2B \over 2 y_p}$

$\boxed{ P+Q = (\lambda^2 - x_p - x_q, - \lambda^3 + \lambda (x_p + x_q) - \nu)}$

Adding points graphically

Adding points can be illustrated by the following picture:

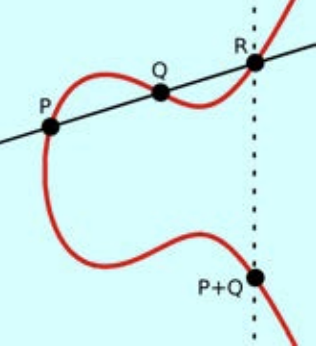
adding points P and Q

Given two points P and Q we can run a line through them and this line intersects the curve at a
third point R. If we mirror R by the x-axis, we find point $P+Q$. When $P = Q$, we take the tangent of this point which also intersects the curve at a third point, which should also be mirrored by the x-axis to get $2P$. When the line is vertical it has an intersection point at infinity, our zero point $[0:1:0]$.

Verifying whether adding points of an Elliptic Curve fulfils the Abelian Group criteria

So, now we would like to check whether the points of the Elliptic Curve in projective space follows the rules given by the Abelian Group.

The five rules of the Abelian Group are (we use $+$ here as this is what we use by definition, $0$ which is the identity point for addition, and we use $P$, $Q$ and $R$ as our points on the Elliptic Curve):

Closure. If $P$ and $Q$ are on the Elliptic Curve, then $P + Q$ is also on the Elliptic Curve. This is obvious considering we have P and Q, draw a line through it and find the third intersection point.
Associativity. The following holds: $ (P + Q) + R = P + (Q + R)$
This appears to be not so obvious and rather complex. I can not verify this by myself. However, very clever people did, and I assume it holds as stated.
Commutativity. The following holds: $ P + Q = Q + P $
Well that is obvious too. We draw a line through P and Q to find the third intersection point. $P + Q$ or $Q + P$, the line is the same.
Identity Element. The following holds: $ P + 0 = P $
This occurs only when P is located on the x-axis. The line is the tangent to the curve and running vertically.
Inverse element. For all points there exists an element $Q$ such that: $ P + Q = 0 $
We can rewrite this as $P = -Q$. Since the curve is symmetric on the x-axis, $Q$ must be the mirrored point of $P$, that is $(x_p, y_p) = (x_r, -y_r)$. In this case the line running through P and -Q is also vertical.

Conclusion

We defined a way to add two points (P and Q) on an Elliptic Curve that results in a third point (R). We also know that the points on an Elliptic Curve form an Abelian Group, so we can do some math on those points.

Footnote: pictures are taken from: Wikipedia